
Galileo sa bránil proti tomu, aby jeho fyzikálne závery (objavy) spochybňovali fyzikálni laici (filozofi) tým, že do fyziky zaviedol okrem požiadavky experimentálneho dôkazu pravdivosti všetkých jeho fyzikálnych argumentov, aj požiadavku, aby všetky fyzikálne argumenty boli opísané matematickým aparátom, čo v praxi znamená iba toľko, aby každý fyzikálny argument bol vyjadrený matematickou rovnicou.
Táto Galileova požiadavka sa vo fyzike ujala a preto do dnešných dní pravdivosť (temer) všetkých fyzikálnych záverov je podložená okrem experimentálnych dôkazov aj matematickými rovnicami. (Iba rovnicami!)
(Relativita zotrvačného pohybu matérie (čiže iba očná ilúzia pohybu matérie) nie je do dnešných dní experimentálne dokázaná, ani matematicky opísaná, nakoľko fyzika do dnešných dni nenašla fyzikálny rozdiel medzi nehybným stavom telies a ich pohybovým stavom. Tým pádom fyzika nenašla ani definíciu pre samotný pohyb matérie, ktorú by vedela dokázať experimentálne a opísať matematickou rovnicou.)
Praktický zmysel tejto Galieovej požiadavky spočíva v tom, že v eventuálne mylných matematických rovniciach, opisujúcich obsah toho ktorého fyzikálneho argumentu, dá sa veľmi ľahko odhaliť aj omyl samotného fyzikálneho argumentu a to bez jeho overenia experimentálnymi dôkazmi.
Z uvedeného dôvodu, eventuálne mylný obsah fyzikálnych argumentov, zvaných ako Práca (A) a Energia (E), musí byť jasne zreteľný už aj v ich matematických rovniciach.
Fyzika definuje svoje dva parametre, Prácu (A) a Energiu (E), ako hodnoty pôsobenia sily (F = m.a) na dráhe (s).
Konkrétnejšie povedané, fyzika definuje veľkosť hodnoty parametrov, Práca (A) a Energia (E), ako súčin sily (F), s dráhou (s), čiže ako nasledovný súčin:
(F.s) = (m.a).(s).
Fyzikom ale za celé obdobie existencie fyziky ušla pozornosti tá objektívna realita, že sila (F), môže posúvať teleso o hmotnosti (m), po dráhe (s), iba vtedy, keď ona pôsobí na teleso počas nie nulového času (t > 0), čiže keď ona pôsobí na teleso ako časový impulz sily:
(F.t) = m.(a.t) = m.v
Aby teleso o hmotnosti (m = 1kg) mohlo prejsť dráhu (s = 5m), zrýchlením (a = 10m/sec.sec), musí naň bezpodmienečne pôsobiť sila (F = m.a), za čas (t = 1sec). Čiže na to aby teleso prešlo dráhu (s = 5m) musí pôsobiť nasledovný časový impulz sily:
(F.t) = (m.a).t = m.v = (1kg.10m/sec.sec).(1sec) = (1kg.10m/sec)
Na konci toho časového impulzu sily (F.t), teleso o hmotnosti (m = 1 kg), nadobudne rýchlosť (v = 10m/sec), respektíve nadobudne hybnosť:
(p =m.v = 1kg.10m/sec)
a pritom prejde (nehmotnú) dráhu (s = 5m).
To je všetko, čo časový účinok sily (F.t) môže vykonať s telesom o hmotnosti (m = 1kg), na ktoré pôsobí zrýchlením (a = 10m/sec.sec), za čas jednej sekundy, (t = 1sec).
Samotná sila (F = m.a), mimo súčinu s časom (t), čiže nie ako časový impulz sily (F.t), nedokáže vôbec nič, preto nedokáže ani pohnúť telesom (m = 1kg), lebo sila (F), mimo súčinu s časom (t), je mimo časová i mimo priestorová sila, ktorá objektívne neexistuje.
Ide iba o predpoklad, iba o možnosť časového účinku sily (F), ale bez udania dĺžky času (t) trvania tejto sily. V skutočnosti ide o túto rovnicu:
(F = F.0t)
Výrok: "Sila (F) je príčinou zrýchleného pohybu matérie", je nepravdivý výrok. To je iba abstraktný (slovný) predpoklad zrýchleného pohybu matérie.
Pravdivý je nasledovný výrok" "Príčinou zrýchlenia matérie, je časový účinok sily (F.t)".
Z uvedeného dôvodu každá matematická rovnica, v ktorej vystupuje sila (F), mimo súčinu s časom (t), čiže nie ako časový impulz sily (F.t), automaticky prezentuje nie len logický, ale aj fyzikálny, mimo časový a mimo priestorový, abstraktný nezmysel: (F = F.0t).

Keďže vo fyzikálnych parametroch, Práca (A), ako aj Energia (E), vystupuje iba a jedine sila (F = F.0t), mimo súčinu s času (t), preto bez diskusie, tieto dva fyzikálne parametre, už aj na prvý pohľad sú nezmyselné fyzikálne parametre, ktoré nemôžu opisovať žiadny zrýchlený pohyb, ale ani iný druh pohybu materiálnych telies v priestore (s) a v čase (t).
Akýkoľvek pohyb matérie (zrýchlený, alebo rovnomerný, či kombinovaný) mimo súčinu s časom (t), v materiálnej prírode neexistuje.
Taký pohyb existuje iba v pomätených hlavách relativistických fyzikov a bodových matematikov.
Vynásobiť objektívne neexistujúcu, preto iba abstraktnú, iba predpokladanú, mimo časovú silu (F.0t), s dráhou (s), ktorú teleso (m) neprešlo:
A = E = (F.0t.s)
a potom ten abstraktný, mimo časový nezmyselný súčin, ešte aj hrdo vyhlásiť za pohybové fyzikálne parametre, za Prácu (A) a Energiu (E), to je jednoznačný prejav duševného defektu toho, kto taký súčin vykonáva, ale aj toho, kto učí takýto súčin vykonávať.
V prípade, že takýto súčin vykonáva dav, ide prejav davovej psychózy, davového duševného defektu. V prípade že taký súčin vykonáva celé ľudstvo, ide o prejav celosvetovej psychózy, čiže duševného defektu celého ľudstva.
Táto skutočnosť preto oprávnene implikuje nevyhnutnú potrebu liečenia ľudstva z predmetnej duševnej psychózy, z predmetného duševného defektu, čiže z násobenia ničoho s ničím, násobenia nehmotného predpokladu s nehmotným predpokladom.
Nezmyselnosť obsahu fyzikálnych parametrov, Práca (A), ako aj Energia (E), jednoznačne dokazuje aj nezmyselný matematický aparát týchto dvoch mimo časových fyzikálnych nezmyslov.
Prvá spoločná (učebnicová) matematická rovnica Práce (A) a Energie (E), je táto rovnica:
A = E = F.s = m.a.s = m.v.v
Aj Einsteinova rovnica Energie:
(E = m.v.v = m.c.c)
je odvodená od tejto rovnice.
V skutočnosti ale ide o nasledovnú matematickú rovnicu:
A = E = F.0t.s = m.(0.v).(0v) = m.c.c = m.0.
Ide o matematický opis nehybného stav telesa.
Druhá spoločná (učebnicová) matematická rovnica Práce (A) a Energie (E), je táto rovnica:
A = E = F.s = 1/2.m.v.v
Z uvedenej rovnice implicitne (následne) vyplýva aj taká, zatiaľ nikým nepovšimutá banalita, že keď hodnota rýchlosti (v), je v obidvoch rovniciach rovnako veľká, potom hodnota prvej rovnice:
A = E = F.s = m.v.v
je dvakrát väčšia, ako hodnota druhej rovnice:
A = E = F.s = 1/2.m.v.v
Ibaže skutočný tvar (aj) tejto rovnice je nasledovný:
A = E = F.0t.s = 1/2.m.(0.v).(0.v) = m.(0.v).(0.v) = m.()
V tomto prípade platí pravidlo, že hodnota rôzne veľkých fyzikálnych nezmyslov je vždy rovnaká, čiže nulová.
(V prípade pôsobenia sily (F), mimo času (t), ako (F = F.0t) na dráhe (s), čiže v prípade pôsobenia mimo časovej sily (F), rôzna veľkosť učebnicovej hodnoty uvedených dvoch, identických rovníc, opisujúcich hodnotu Práce (A) a Energie (E), čiže mimo časový (preto nezmyselný) účinok sily (F = F.0t), na dráhe (s), už by nemala nikoho prekvapiť.)
Tretia spoločná učebnicová matematická rovnica Práce (A) a Energie (E), je táto rovnica:
A =∫F.(ds) = ∫m.a.(ds) = m.∫(dv/dt).(ds)
(Pritom všetky tieto tri rovnice dávajú identicky, čiže úplne rovnaký (nezmyselný) výsledok!!!)
Túto tretiu matematickú rovnicu Práce (A) a Energie (E), Galileo ešte nemohol poznať a preto ani posúdiť jej hodnovernosť (jej pravdivosť).
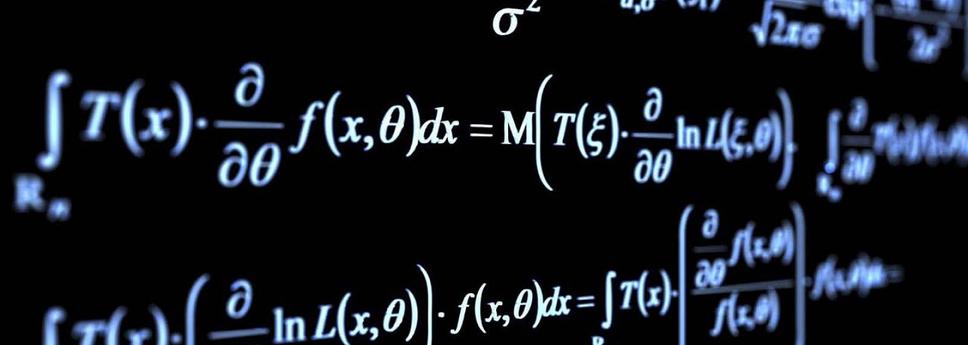
To preto lebo táto rovnica Práce (A) a Energie (E), je v takzvanom integrálnom (diferenciálnom) tvare. Diferenciálny počet vymyslel až neskôr Izák Newton.
V tejto rovnici je vyjadrené zrýchlenie (a) ako prvá derivácia rýchlosti (v) podľa času (dt):
a = (dv/dt)
Pričom ale hodnota (dv) nie je uvedená ako funkcia času (t). Pritom podmienkou derivácie hoci čoho, podľa času (dt) je to, aby to hocičo bolo vyjadrené ako funkcia času (t).
Po pochopení objektívnej reality spojenej s účinkami (objektívne neexistujúcej) mimo časovej sily: (F = F.0t), na dráhe (0.s), ktorú teleso o hmotnosti (m) neprešlo, čiže:
F.s = F.0t.(0.s) = m.(a.0t).(0.s) = m.0.(0.s) = m.0!!!
pokračovanie tohto článku už nemá zmysel, lebo analyzovať to, čo objektívne neexistuje, to je ako šiť šaty z neviditeľnej látky, neviditeľnou ihlou a neviditeľnou niťou, za čo najkratší čas. Alebo ako nasýtiť sa klobásami z medveďa, ktorého ešte nikto nevidel, ktorého si vieme iba predstaviť.
Zmyslom pokračovania tohto článku je poukázať na to, že aj pri akceptácii učebnicových, neexistujúcich, preto nezmyselných účinkov mimo časovej sily (F = F.0t), na matériu (m), nedá sa dopracovať k takým matematickým rovniciam, akými učebnice fyziky a matematiky opisujú hodnoty, Práce (A) a Energie (E).
Zmyslom pokračovania tohto článku je poukázať na to, že k učebnicovým hodnotám Práce (A) a Energie (E), dá s dopracovať iba a jedine matematickým podvodom.
Fyzika opisuje hodnotu Práce (A) a Energie (E), aj touto rovnicou:
A = E =∫F.0t.(ds) = ∫m.a.(ds) = m.∫(dv/dt).(ds)
Prvým problémom tejto (mimo časovej, nezmyselnej, učebnicovej) diferenciálnej rovnice (okrem iného) je aj to, že ona deriváciu rýchlosti (dv) podľa času (dt)
a = (dv/dt)
iba naznačuje, ale ju nevykonáva, lebo neuvádza konečnú hodnotu, naznačenej derivácie, diferenciálu rýchlosti (dv), podľa diferenciálu času (dt).
To nikto nemôže robiť dovtedy, kým hodnotu (dv) nie je je schopný vyjadriť ako funkciu času (t).
(Zrýchlenie (a) vyjadrené v diferenciálnom tvare ako funkcia času (t), vyzerá nasledovne:
dv = a.dt
ds = a(t.dt).
Potom platí:
a = (dv)/(dt)
a = (a.dt)/(dt) = a.1 = a.
A = E = (F.0t).(s) = m.a.∫.(t.dt) = (m.a).(a.1/2.t.t) = (F.s)
Táto mimo časová rovnica vyhýba sa tej, pre fyziku a matematiku veľmi nepríjemnej skutočnosti, že prečo ona prezentuje iba mimo časový účinok sily (F = F.0t), a že prečo hodnotu (dv) nedokáže, nemôže vyjadriť, ako funkciu reálneho času (t), keď na prekonanie dráhy (s = a.1/2.t.t), sila (F) musela na teleso (m), bezpodmienečne pôsobiť čas (t), ako impulz sily: (F.t)
Keď hodnotu dráhy (s) je vyjadrime ako funkcia reálneho času (t), tak rovnica dráhy (s) vyzerá nasledovne:
s = (a.1/2.t.t)
Z tejto rovnice vyplýva hlavne to, že jej dĺžka (s = 5m) mohla vzniknúť iba a jedine tak, že ju prešlo teleso (m = 1kg), ktoré tlačila sila (F), ako časový impulz sily (F.t) zrýchleným pohybom (a = 10m/sec.sec), za dobu (t = 1sec).
Z toho implicitne vyplýva aj to, že na to teleso musel pôsobiť iba časový impulz sily (F.t), nasledovne:
F.t = m.a.t = (m.a).(d.d)(1/2.t.t)/(dt.dt).t)
F.t = m.a.t = (m.a).t
Ibaže výsledkom časového impulzu sily (F.t) na teleso (m), už by nebola, Práca (A) ani Energia (E), ale iba a jedine hybnosť telies:
F.t = m.a.t = m.v
Súčin časového impulzu sily (F.t) s dráhou (s = 5m), dával by takýto výsledok:
(F.t).(s) = m.a.t.s = 1kg.(10m/sec.sec).(1sec).(5m)
(F.t).(s) = 1kg.(10m.5m/sec)
(F.t).(s) = 1kg.(10m/sec).5m = m.v.s
Tento výsledok ale nie je zhodný s učebnicovou hodnotou Práce (A), ani s hodnotou Energie (E):
A = E = 1/2.m.v.v
Tento výsledok je ale zhodný s hodnotou Práce (A) a hodnotou Energie (E) v tom, že je rovnako nezmyselný.
Túto kardinálnu chybu, obsiahnutú v učebnicovej, mimo časovej matematickej rovnici, Práce (A), ako aj Energie (E), využil prvý (neznámy, anonymný) matematický podvodník, či matematický tupec, na neprípustnú matematickú úpravu v nasledujúcej rovnici:
A = E = F.s = m.∫(dv/dt).(ds)
Ten matematický podvodník, či matematický tupec, (platí oboje naraz) z nevykonanej derivácie rýchlosti (v), podla času (dt), ale iba z naznačeného zrýchlenia (a = dv/dt), presunul hodnotu (dt) pod hodnotu (ds), nasledovným podvodným spôsobom:
A = m.∫(dv/dt).(ds)
A = m.∫(dv).(ds/dt)
Tým ale radikálne zmenil zmysel tejto rovnice.
Takto postupujú iba matematickí Hurvínkovia, ako aj (nie len) zamestnanci Matematického Ústavu SAV.
Potom slávnostne prehlásil, že našiel rovnicu Práce (A) a Energie (E), čiže rovnicu výsledku účinku pôsobenia sily (F = F.0t)), mimo času (t), na dráhe (s), v nasledujúcom matematickom tvare:
A = E = m.∫(v).(dv)
následne túto rovnicu integroval a vyšlo mu toto:
A = E = m.1/2(v.v).
A = E = 1/2.m.(v.v).
Čo sa konkrétne v materiálnej prírode pohybuje súčinom dvoch rovnako veľkých rýchlosti: (v.v), ktoré na viac nie sú zhodné s hybnosťami telies: (p = m.v), to matematického podvodníka nezaujímalo, podobne ako to nezaujíma ani súčasných fyzikálnych a matematických podvodníkov.

Od čias toho matematického podvodníka, nikoho nenapadlo prekontrolovať správnosť jeho podvodníckeho postupu tvorby rovnice Práce (A) a Energie (E).
Túto rovnicu dvoch fyzikálnych nezmyslov, zvaných ako Práca (A) a Energia (E, Ek), do dnešných dní, každý jeden matematik, ako aj fyzik, automaticky považuje za pravdivú rovnicu, i keď už aj matematický postup vytvorenia tejto rovnice porušuje všetky logické, fyzikálne, ale hlavne matematické pravidlá.

Táto skutočnosť exaktne dokazuje to, že nikto na svete (okrem jednej Výnimky)

nechápe podstatu diferenciálneho počtu a preto nikto na svete, okrem veľmi skromného, hanblivého, až cudného občana Výnimku, nie je schopný konštruktívne kriticky reagovať na matematické nezmysly ktoré odporujú nie len časo - priestorovým fyzikálnym zákonom, ale aj samotným (pochybným) zásadám diferenciálneho počtu.
Pre lepšie pochopenie problému, uvediem učebnicový matematický zápis rovnice mimo časového fyzikálneho nezmyslu, zvaného Práca (A) a Energia (E), podľa tých pravidiel, ktoré používa relativistická fyzika a bodová matematika.
Matematická rovnica dráhy (s), ako funkcia času (t), vyzerá nasledovne:
s = 1/2.a.(t.t)
Táto rovnica ale hovorí aj o tom, že aký dlhý čas (t) sila (F), ako časový impulz sily (F.t), tlačila teleso o hmotnosti (m) zrýchlením (a) po dráhe (s):
(F.t) = (m.a.t) = m.(a.t) = m.v
Takže dĺžku tej dráhy (s):
s = 1/2.a.(t.t)
nemohla vytvoriť mimo časová sila (F = F.0t), ale iba časový impulz sily (F.t).
Aj dráha (s) v tvare (s = v.t), je funkciou času (t) a preto aj ona naznačuje dĺžku času (t) za ktorý teleso (m) prešlo tú dráhu (s) rýchlosťou (v.t).
Dráha iba v tvare (s = 5m), nie je funkciou času (t), preto lebo ona je iba predpokladaná vzdialenosť, ktorú teleso ešte neprešlo, pretože nemohlo sa pohybovať po tej dráhe mimo časovou (neexistujúcou) silou (F = 0.t) za čas (t).
Takže nie každá dráha (s), ktorá má rovnakú dĺžku, má aj rovnakú matematickú, časo - priestorovú rovnicu!
No a teraz preveďme analýzu postupu výpočtu veľkosti Práce (A) a Energie (E), podľa nasledovnej učebnicovej rovnice:
A = E = F.∫ds
A = E = m.a.∫ds
Integrácii nepodliehajú konštanty (m) a (a), preto ich môžeme dať pred znak integrálu (∫). Nech (s) jed dráha, ktorú nevieme vyjadriť ako funkciu času, lebo ju žiadne teleso neprešlo v čase (t), potom platí:
A = E = m.a∫ds
A = E = m.a.s
Pre hodnoty:
a = 10m/sec.sec
s = 5m
t = sec
dostaneme nasledovný výsledok:
A = E = m.(10.m/sec.sec).(5m)
A = E = m.(10m.5m)/(sec.sec)
A = E = m.(10m/sec).(5m/sec)
A = E = m.(v1 = 10m/sec).(v2 = 5m/sec)
Okrem toho že dostaneme úplne nezmyselný výsledok, ktorým sa nič v prírode nepohybuje, na viac ten nezmyselný výsledok nie je ani súčinom dvoch rovnako veľkých rýchlosti (v.v), ako to vyžaduje učebnicová rovnica Práce (A) a Energie (E):
A = E = 1/2m.(v.v)
Aj keď napíšme rovnicu účinku mimo časovej sily (F = F.0t), na dráhe (s) ktorá je funkciou času (t):
s = (a.1/2.t.t ) = (10m/sec.sec).(1/2.1sec.1sec) = (5m)
ani vtedy nedostaneme učebnicami fyziky hlásaný výsledok
A = E = 1/2m.(v.v)
Lebo platí:
(dv = a.dt)
(ds = a.t.dt)
A = E =∫F.ds
A = E = m∫(dv/dt) . (ds)
A = E = m∫(a.dt)/(dt) . (ds)
A = E = m∫(a).a(t.dt)
A = E = (m.a)∫a.(t.dt)
A = E = (m.a).(a.1/2.t.t)
A = E = 1kg.(10m/sec.sec).(10m/sec.sec.1/2.(1sec.1sec)
A = E = 1kg.(10m/sec.sec).(1/2.10m = 5m)
A = E = 1kg.(10m.5m)/(sec.sec)
A = E = (v1 = 10m/sec).(v2 = 5m/sec)
Vždy dostaneme iba súčin dvoch rôzne veľkých rýchlosti (v1. v2),
Pritom matematika z čuda zvaného plošné (obdlžníkové zrýchlenie):
(10m.5m)/(sec.sec)
dokáže (nevedno prečo na na akom matematickom základe) vyrobiť ďalšie matematické čudo a to súčin dvoch rovnomerných rýchlosti, čiže nezmyselnú (obdĺlžníkovú rýchlosť):
(v1 = 10m/sec).(v2 = 5m/sec)
Vyrábať takéto matematické čudá, to si vyžaduje poriadnu dávku matematickej drzosti, ktorá má kryť matematickú tuposť matematikov.
Preto aj rovnica mimo časového účinku sily (F = F.0t), aj na časovej dráhe, s = f(t), čiže rovnica Práce (A), ako aj rovnica Energie (E):
A = E = 1kg.(v1 = 10m/sec).(v2 = 5m/sec)
jednoznačne prezentujú iba matematické drzosti (matematické tuposti) jedincov mentálne nedostatočných na matematiku, teda aj (nie len) zamestnancov MÚ SAV,
ktorí sa ale takejto objektívnej klasifikácii ich matematických (ne)vedomosti, ani vo sne nemienia brániť.
Záverečné konštatovanie!
Žiadnym rozumným matematickým aparátom nedá sa dopracovať k učebnicovému výsledku rovnice mimo časového účinku sily (F), na dráhe (s), čiže k hodnote súčinu mimo časovej sily (F = F.0t), s dráhou (s) a preto ani k učebnicovej rovnici, Práce (A), ale ani k rovnici akejkoľvek Energie (Ek), (Ep), (E) v tvare:
A = E = 1/2.m.v.v
Lebo správnym matematickým postupom dopracujeme sa vždy a jedine iba k výsledku:
A = E = m.v1.v2
nikdy však nie k učebnicovému výsledku:
A = E = 1/2.m.v.v
Výsledok rozboru matematického aparátu mimo časového účinku sily (F = F.0t) na dráhe (s), čiže výsledok rozboru matematických rovníc, Práce (A) a Energie (E), jednoznačne dokazuje to, že samotné fyzikálne pojmy, Práca (A) a Energia (E), sú logické, ako aj fyzikálna nezmysly, lebo oni svojvoľne deformujú jediný možný, jedine objektívne reálny výsledok časového pôsobenia sily (F.t), na dráhe (s), a to hybnosť telies:
p = m.v
na objektívne neexistujúce fyzikálne nezmysly zvané, Práca (A) a Energia (E), čiže na mimo časové účinky sily (F = F.0t) na dráhe (s), ktoré telesá nikdy neprešli a ktoré sú na viac vyjadrené mylnou (podvodníckou) matematickou rovnicou:
A = E = 1/2.m.v.v.
Tieto učebnicové fyzikálne nezmysly, čiže mimo časové účinky sily (F = F.0t), na dráhe (s), nedajú sa dosiahnuť správnymi matematickými postupmi, ale iba matematickými podvodmi.
Podvodom bola dosiahnutá aj Einstenova rovnica Energie (E = m.c.c).
Otec vodíkovej bomby, Leo Silárd, veriac Einsteinovej rovnici (E = m. c.c), pred jej prvým výbuchom, odsťahoval sa na druhý koniec USA. Ibaže veľkosť energie výbuchu vodíkovej bomby nepotvrdila správnosť Einsteinovej rovnice (E = m.c.c). A ani nemohla, lebo tá bomba nechodila do školy a ani na univerzitu.
Preto celá relativistická fyzika, ako aj bodová matematika, je podvodnícka a všetci učitelia matematiky a fyziky sú podvodníci, alebo na výkon ich povolania mentálne nedostatoční jedinci (čiže matematickí a fyzikálni papagáji).
Ja sa oprávnene prikláňam k druhej (papagájskej) verzii.
Na tú mentálnu mizériu učiteľov matematiky a fyziky najviac doplácajú študujúci občania SR, lebo je veľmi ťažké akceptovať (naučiť sa) nezmyselné, nelogické, podvodnícke, mimo časové fyzikálne a matematické argumenty, ako pravdivé zákony, časo - priestorovej materiálnej prírody.
Článok sa priebežne zdokonaľuje.







